Inhaltsverzeichnis
Klassen/Objekte mit Attributen
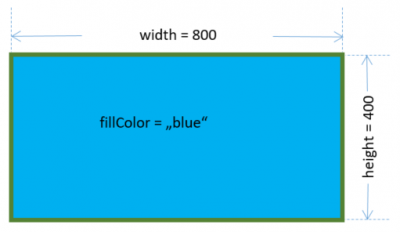Ein Attribut eine Objektes ist eine Eigenschaft, die einen Wert annehmen kann. Im Bild rechts etwa ist ein Objekt der Klasse Rectangle zu sehen mit den Attributen width (Wert: 800), height (Wert: 400) und FillColor (Wert: blue). Es kann viele weitere Objekte derselben Klasse geben. Sie haben die selben Attribute (width, height, …), aber diese können andere Werte haben.
Siehe dazu auch das Kapitel "Grundbegriffe der Objektorientierung".
Beispiel 1: Die Klasse Person
Wir beginnen mit einem künstlichen - dafür aber sehr einfachen - Beispiel: Einer Klasse Person mit den Attributen name und geschlecht (Datentyp: String) sowie größe (Datentyp: double, gemeint ist: in m).
Unter Programmierern ist es Konvention Attribute mit Kleinbuchstaben zu beginnen. Attributbezeichner dürfen keine Leerzeichen enthalten. Setzt sich ein Attribut aus mehreren Wörtern zusammen, so trennt man sie entweder mit Unterstrichen (weniger üblich, z.B. handbreite_in_cm) oder verwendet Großschreibung mitten im Wort (camel case, auf deutsch: Binnenmajuskel, z.B. handbreiteInCm).
Deklaration von Attributen:
Attribute werden deklariert, indem man auf oberster Ebene innerhalb der Klassendeklaration (also nicht innerhalb einer Methode!) den Datentyp des Attributs gefolgt von seinem Bezeichner schreibt, z.B.
class Person {
String name;
String geschlecht;
double größe;
}
Es ist auch möglich, bei der Attributdeklaration einen Anfangswert anzugeben, z.B.
String geschlecht = "weiblich";
Auf die Attribute von Objekten kann man außerhalb der Klassendeklaration mithilfe der Punktschreibweise zugreifen. Wie das geht, siehst Du im obigen Beispiel in den Zeilen 2 - 12.
Beispiel 2: Klassen mit Attributen und Methoden
Attributdeklarationen und Methodendeklarationen dürfen innerhalb einer Klassendeklaration beliebig hintereinander stehen. Es ist aber üblich, gleich zu Beginn einer Klassendeklaration alle Attribute der Klasse zu deklarieren und danach erst die Methoden.
class Person {
String name;
String geschlecht;
double größe;
// Jetzt kommt eine Methodendeklaration:
void schreibeName(){
println(name);
}
}
Innerhalb von Methodendeklarationen kann man auf Attribute wie auf gewöhnliche Variablen durch Angabe ihres Bezeichners zugreifen. Du siehst das im obigen Beispiel in der Anweisung println(name). Ausgegeben wird der Wert des Attributs Name desjenigen Objekts, für das die Methode aufgerufen wurde.
Du fragst Dich vielleicht, wie der Compiler Attributdeklarationen und Methodendeklarationen unterscheiden kann?
Den Unterschied macht die runde Klammer hinter dem Bezeichner einer Methode. Jetzt ist Dir sicher auch klar, weshalb bei Methoden ohne Parameter trotzdem die runden Klammern () benötigt werden.
Führe das Programm schrittweise mit "step into (
)" aus und beobachte, welchen Wert die Attribute name und geschlecht jeweils innerhalb der Methoden haben! Öffne dazu rechts den Variablen-Reiter. Die Objekte werden jeweils im "zugeklappten" Zustand gezeigt. Klappe sie auf!
Wenn sich der Aktuelle Ausführungspunkt des Programms (grün hinterlegte Programmzeile) gerade innerhalb einer Methode befindet, wird das Objekt, für das die Methode aufgerufen wurde, immer mit this bezeichnet. Klappe daher auch das this-Objekt im Reiter "Variablen" auf und schau' Dir seine Attributwerte an.
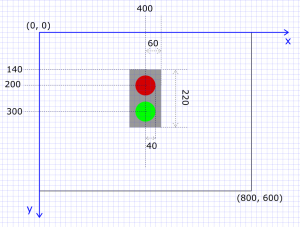
Beispiel 4: Ampel
Wir programmieren eine Klasse Ampel, die eine einfache Fußgängerampel Zeichnet und Methoden schalteGrün() und schalteRot() zum Umschalten besitzt. Die Ampel besteht aus einem Rectangle-Objekt und zwei Circle-Objekten. Diese speichern wir als Attribute der Klasse Ampel. Sie werden in der Methode init() instanziert und initialisiert.
Ich habe Dir noch etwas Arbeit im Programm hinterlassen (siehe die Kommentare). Vielleicht möchtest Du die Ampel auch noch etwas umfangreicher gestalten:
- Umgib das Gehäuse mit einem dunkelgrauen Rahmen (Methode
setBorderColorderRectangle-Klasse!) - Füge ein gelbes Licht hinzu!
- Füge eine "Fuß" hinzu!
Aufgabe 1: Tiere
Erstelle eine Klasse Tier mit den Attributen art (Typ String), name (Typ String) und beinzahl (Typ int) sowie einer Methode vorstellen(), die im Falle der Katze Snoopy (mit zum Glück noch 4 Beinen) folgende Meldung ausgibt:
Ich heiße Snoopy und bin ein/e Katze mit 4 Beinen.
Aufgabe 2: Längeneinheiten
Sind Dir schon mal Längenangaben wie 12 in oder 17 zoll oder 14'' begegnet? Sie bezeichnen dieselbe Längeneinheit Inch (im deutschen auch als "englischer Zoll" bezeichnet) und werden in Deutschland bespielsweise zur Angabe von Monitor-Diagonalen verwendet. In England und den USA sind sie neben den international vereinbarten SI-Einheiten bis heute weit verbreitet.
Umrechnung: 1 in = 2.54 cm
Schreibe eine Klasse Länge mit den Methoden speichere(double länge, String einheit), schreibeInch() und schreibeCm(), die bei der Umrechnung der beiden Längeneinheiten hilft. Hier ein beispielhaftes Hauptprogramm zusammen mit der Ausgabe, durch das die Bedeutung der Methoden klar wird:
Programm:
Länge a = new Länge(); a.speichere(3.0, "inch"); a.schreibeCm(); a.speichere(25.4, "cm"); a.schreibeInch();
Ausgabe
7.62 cm 10 inch
Tipp: Natürlich benötigt die Klasse auch ein Attribut, um die Länge zu speichern. Es bietet sich an, nur ein einziges Attribut zu deklarieren, in dem die Länge immer in cm gespeichert wird und nur beim Speichern von inch und der Ausgabe in inch umzurechnen.
Aufgabe 3: RechteckHelfer
Schreibe eine Klasse RechteckHelfer mit den Methoden setzeLängeBreite(double länge, double breite), gibUmfang(), gibFlächeninhalt() und gibDiagonalenlänge(). Hier ein Hauptprogramm mit Ausgabe, das die Bedeutung der Methoden zeigt:
Programm:
RechteckHelfer rh = new RechteckHelfer(); rh.setzeLängeBreite(3, 4); println(rh.gibUmfang()); println(rh.gibFlächeninhalt()); println(rh.gibDiagonalenlänge());
Ausgabe
14 12 5
Tipp: Natürlich benötigt die Klasse auch zwei Attribute, um die Länge und Breite des Rechtecks zu speichern!
Aufgabe 4: Eine Klasse zum Bruchrechnen
Studiere die Klasse Bruch im Programm unten genau und ergänze folgende Methoden:
subtrahiere(Bruch b2)multipliziere(Bruch b2)dividiere(Bruch b2)gibAusEcht()(gibt den Bruch ggf. als echten Bruch aus, also 3 1/2 statt 7/2)erweitere(int faktor)
Für die Mathematik-Interessierten unter Euch:
Algorithmus zur Berechnung des größten gemeinsamen Teilers zweier Zahlen
In der Methode kürzen wird der größte gemeinsame Teiler von Zähler und Nenner berechnet. Die Strategie ist eine vereinfachte Variante des Euklidischen Algorithmus und basiert auf folgendem einfachen Satz:
Wenn eine Zahl $x$ ein Teiler der Zahlen $a$ und $b$ ist, dann ist $x$ auch ein Teiler von $|a - b|$ und von $a + b$.
In Folgenden ein Beispiel zur Durchführung des Algorithmus, das - basierend auf dem eben genannten Satz - auch den Korrektheitsbeweis des Algorithmus skizziert:
Wir bestimmen den ggT von $24$ und $80$ (und nennen ihn im Folgenden kurz $x$).
- $x$ ist Teiler beider Zahlen und teilt daher auch $80 - 24 = 56$. Wir nehmen jetzt die kleineren beiden dieser drei Zahlen (also $24$ und $56$) und setzen das Spiel damit fort.
- $x$ ist Teiler von $24$ und $56$ und teilt daher auch $56 - 24 = 32$. Wir nehmen jetzt die kleineren beiden dieser drei Zahlen (also $32$ und $24$) und setzen das Spiel damit fort.
- $x$ ist Teiler von $32$ und $24$ und teilt daher auch $32 - 24 = 8$. Wir nehmen jetzt die kleineren beiden dieser drei Zahlen (also $24$ und $8$) und setzen das Spiel damit fort.
- $x$ ist Teiler von $24$ und $8$ und teilt daher auch $24 - 8 = 16$. Wir nehmen jetzt die kleineren beiden dieser drei Zahlen (also $16$ und $8$) und setzen das Spiel damit fort.
- $x$ ist Teiler von $16$ und $8$ und teilt daher auch $16 - 8 = 8$. Wir nehmen jetzt die kleineren beiden dieser drei Zahlen (also $8$ und $8$) und sind fertig, denn wir wissen jetzt, dass der ggT von $24$ und $80$ ein Teiler von $8$ ist. Gleichzeitig ist aber $8$ auch ein Teiler von $24$ und $80$, teilt also auch deren ggT. Daher ist $8$ der gesuchte ggT.
- Halt, halt, nicht so schnell!!
Warum ist $6$ auch ein Teiler von $24$ und $80$?
Denk' Dir einfach alle Schritte wieder rückwärts: die $8$ teilt $8$ und $8$, also teilt sie auch die Summe $16 = 8 + 8$. Da sie also die $8$ und die $16$ teilt, teilt sie auch $8 + 16 = 24$. Da sie $8$ und $24$ teilt, teilt sie auch $8 + 24 = 32$, usw. Am Ende all dieser Schritte steht fest: $8$ teilt auch $24$ und $80$.
Aufgabe 5: Bild mit verschiedenen Tageszeiten
Die Klasse Bild zeichnet das Bild einer Wüste mit Sonne und Himmel (s.u.) zu drei verschiedenen Tageszeiten. Sie besitzt die Methoden init() (zum Instanzieren und Initialisieren der Objekte), schalteMorgen() (schaltet auf das "Morgenbild" um), schalteMittag() und schalteAbend().
Tipp: Orientiere Dich beim Programmieren am Ampel-Beispiel oben!