Inhaltsverzeichnis
Objekte erzeugen und verändern
Bevor wir eigene Klassen programmieren lernen wir, wie wir Objekte zu bereits bestehenden Klassen erzeugen können. Wir beginnen mit Grafikklassen wie Rectangle oder Circle, weil man die grafische Repräsentation dieser Objekte gleich am Bildschirm sieht.
Objekte instanzieren ( = erzeugen)
Im folgenden Programm erzeugen wir zwei Circle-Objekte und ein Rectangle-Objekt. In Java verwendet man dazu den Operator new gefolgt vom Bezeichner der Klasse und - in Klammern - zusätzlichen Angaben (Parametern), die zum Erzeugen des Objekts benötigt werden.
Durch die Anweisung new Circle(400, 200, 100) wird ein neues Objekt der Klasse Circle (also ein Kreis-Objekt) instanziert ( = erzeugt ). Die Angaben in Klammern nennt man Parameter. Durch sie übermittlen wir dem Objekt die Informationen, die es zur Erzeugung braucht, im Falle eines Circle-Objekts sind dies die Koordinaten des Mittelpunkts und der Radius. Beim Objekt der Klasse Rectangle sind die Parameter die Koordinaten der linken oberen Ecke, die Breite und die Höhe des Rechtecks.
Zur Veranschaulichung siehst Du rechts oben eine Skizze des Zeichenbereichs.
Beachte: Der Ursprung des Koordinatensystems liegt im Zeichenbereich links oben, die y-Achse zeigt nach unten! (Hier die Erklärung dafür.) Falls nichts anderes angegeben wird, liegt der rechte Rand des Zeichenbereichs bei x = 800, der untere bei y = 600.
Methoden aufrufen
Wir wollen die Füllfarbe eines Kreises, seine Größe, Position usw. verändern indem wir Methoden des Circle-Objekts aufrufen. Dazu weisen wir das Objekt (eigentlich: eine Referenz darauf, siehe später) einer Objektvariablen zu:
Circle k = new Circle(250, 200, 100);
Der Datentyp der Objektvariable k ist Circle, weil sie auf ein Circle-Objekt verweist. Genaugenommen liegt das Circle-Objekt irgendwo im Arbeitsspeicher Deines Computers und k enthält die Anfrangsadresse dieses Speicherbereichs. Mithilfe der Punktschreibweise können wir jetzt Methoden des Circle-Objekts aufrufen:
Führe das Programm in Einzelschritten aus ("Step over": 
) und ergänze dann ab Zeile 4 selbst weitere Methodenaufrufe!
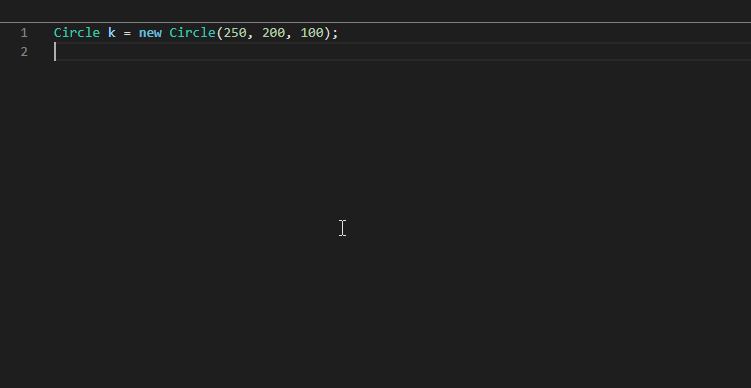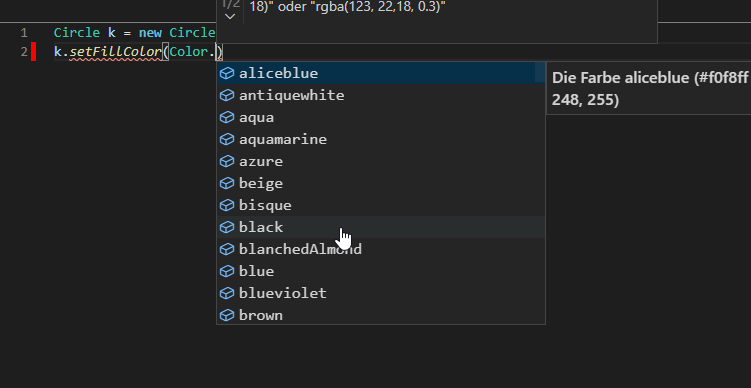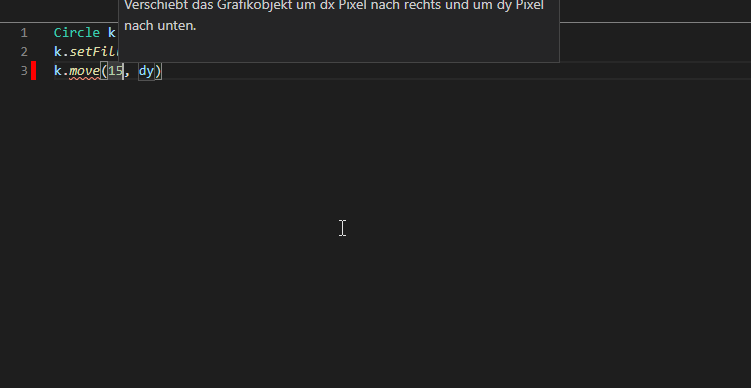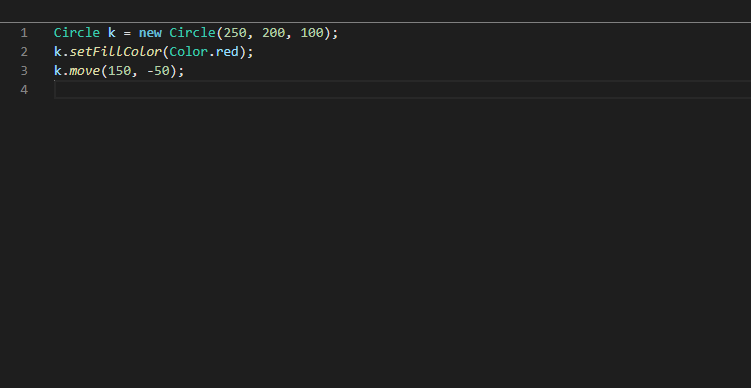
Der Editor hilft Dir beim Tippen, indem er Dir basierend auf Deinen Eingaben laufend Vorschläge macht (code completion, siehe das kleine gif-Video unter diesem Text). Du kannst die Vorschläge mit den Tasten Pfeil rauf/Pfeil runter auswählen und mit der Tabtaste oder der Enter-Taste übernehmen. Bei der Übernahme einer Methode fügt der Editor dann Platzhalter für die Parameter ein (z.B. "Color", "alpha", …). Mit der Tab-Taste springst Du von einem Parameter zum nächsten.
Beispiel 1: Rakete
Mit dem Gelernten können wir jetzt schon kleine Animationen erstellen:
Verbesserung: Group-Objekt
Dass im obigen Programm die Bestandteile der Rakete einzeln verschoben werden müssen, ist sehr ungünstig. Bei langsamer Ausführungsgeschwindikeit sieht man die Teile sogar einzeln vorwärtsruckeln. Und stell' Dir vor, wir wollten die Rakete um ihren Schwerpunkt drehen: Was würde passieren, wenn ab Zeile 11 steht:
spitze.drehen(2); tank.drehen(2); triebwerk1.drehen(2); triebwerk2.drehen(2);
Probier' es doch mal aus (Copy/Paste…)!
Die Lösung der Probleme besteht darin, die einzelnen Objekte zu gruppieren, genauso wie in vektororientierten Zeichenprogrammen. Zu diesem Zweck gibt es die Klasse Group:
Genaue Betrachtung: Objektreferenzen und Objekte
Schau' Dir folgendes Beispielprogramm an:
Wie viele Rectangle-Objekte gibt es in diesem Programm? Was bewirkt die Anweisung k = r?
Zum Vergleich ein ähnliches Programm mit int-Variablen:
Was gibt das Programm aus?
Eine ausführliche Erklärung für dieses merkwürdige Phänomen findest Du auf dieser extra-Seite.
Instanzieren der "Welt"
Damit graphische Objekte ausgegeben werden können, muss zunächst die Grafikausgabe "geöffnet" werden. Dies geschieht durch Instanzieren eines Objektes der Klasse World, z.B.:
new World(800, 600);
Die übergebenen Koordinaten (800, 600) sind die Koordinaten der rechten unteren Ecke der Welt. Dabei ist zu beachten, dass die positive y-Achse - wie bei Computersystemen meist üblich - nach unten zeigt. Hier eine des Welt-Koordinatensystems:
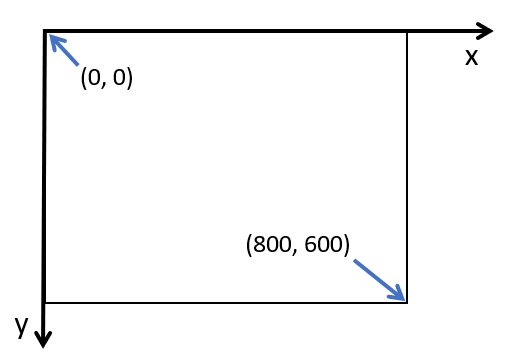
Falls Du vergisst, ein Welt-Objekt zu instanzieren, wird das vom System automatisch nachgeholt, sobald das erste graphische Objekt instanziert wird. In diesem Fall werden die Grenzen des Koordinatensystems automatisch (wie oben) bei x = 800 und y = 600 gesetzt.
Beispiel 2: gedrehte Rechtecke
Jedes der 36 Rechtecke hat initial dieselbe Position. Das erste wird um 10° um mit Drehpunkt (400,300) gedreht, das zweite um 20°, das dritte um 30° usw. Hier eine Schemadarstellung:
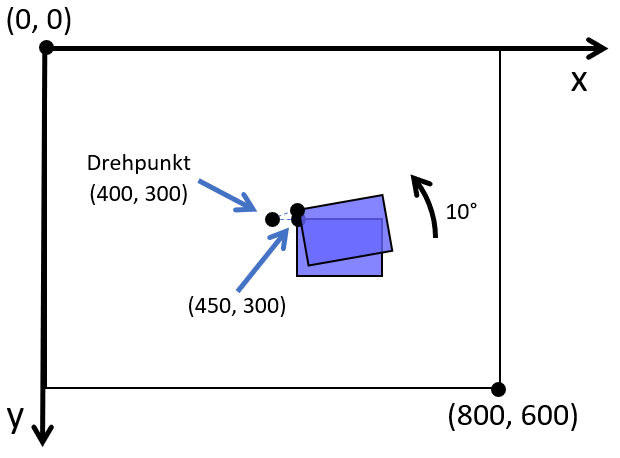
Beispiel 3: Sinuskurve
Die Parameter beim Instanzieren von Circle-Objekten haben folgende Bedeutung: Circle(mitteX, mitteY, radius). Die x-Koordinate erhöht sich von Kreis zu Kreis in 10'er Schritten, der Radius bleibt konstant 20. Der Term für die y-Koordinate 300 + 200*Math.sin(i/5.0) sorgt für die sinusförmige Kurve.
Beispiel 4: Farbige Rechtecke
Neue Farben "mischen":
Du kannst nicht nur die vorgegebenen Farbwerte (Color.red, Color.yellow, …) verwenden, sondern auch beliebige andere Farben erzeugen, indem Du den Rot-, Grün- und Blauwert der Farbe angibst. Die einzelnen Werte dürfen dabei zwischen 0 und 255 liegen. Das folgende Programm erzeugt ein Rechteck-Objekt und färbt es mit einer Farbe, deren Rotwert 100, Grünwert 20 und Blauwert 87 beträgt.
Rectangle r = new Rectangle(10, 10, 100, 100); r.setFillColor(new Color(100, 20, 87));
Wie kommen die Farben zustande?
Computerdisplays bedienen sich eines Tricks zur Farbdarstellung: Da das menschliche Auge nur Farbsensoren für rotes, grünes und blaues Licht hat ("Zäpfchen" auf der Netzhaut), reicht es, nur diese drei Sensortypen einzeln in unterschiedlicher Intensität zu aktivieren, um alle für den Menschen sichtbaren Farbeindrücke hervorzurufen.
Displays bestehen daher aus vielen sehr kleinen roten, grünen und blauen Punkten, deren Helligkeit einzeln geregelt werden kann. Je drei davon werden zu einem Bildpunkt ("Pixel") zusammengefasst. Die Angabe der Rot- Grün- und Blauwerte oben regelt die Helligkeit der jeweiligen Teilpunkte des Pixels. Dabei steht der Wert 0 für "Bildpunkt schwarz" und 255 für "Bildpunkt hat maximale Helligkeit".
Die vom Auge wahrgenommene Farbe des Pixels entspricht der additiven Mischfarbe der drei Teilpunkte. Diese Art der Farbmischung wird für dich ungewohnt sein, weil die Mischfarben von Farbstiften und Wasserfarben subtraktiv zustandekommen. Eine gute Erklärung der beiden Arten von Farbmischung findest Du in den Wikipedia-Artikeln zu additiver und subtraktiver Farbmischung.
Kleines Experiment:
Halte ein Fernglas in umgedrehter Richtung ganz nah an den Bildschirm, dann kannst Du die roten, grünen und blauen Punkte deutlich sehen. Schau' Dir so verschiedenfarbige Flächen am Bildschirm an und beobachte die Intensität der farbigen Teilpunkte.
Aufgabe 1: "Auto"
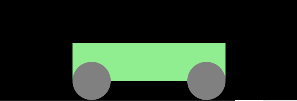Schreibe ein Programm, das ein einfaches Auto (siehe Bild rechts) zeichnet und es dann von links nach rechts fahren lässt!
Aufgabe 2: Farbkreise
Schreibe ein Programm, das drei Farbkreise wie im folgenden Video zeichnet und dann drehen lässt!
